BODMAS Questions With Answer PDF [Class 4, 5, 6, 7, 8, 9, 10]

BODMAS (÷, ×, +, -) is an abbreviation used in mathematics to remember the order of operations. BODMAS stands for Bracket, Order, Division, Multiplication, Addition, and Subtraction. To solve operations in mathematics, we have to follow certain rules. If we do not adhere to these rules, we may not be able to answer the given question correctly. That is why we are taught to follow the BODMAS rule from a young age.

Today, we will explore BODMAS-related questions and their corresponding answers. Additionally, you will learn how to solve mathematical expressions step by step. also, I will provide you BODMAS Questions With Answer PDF.

BODMAS Symbols and Meaning

B	Brackets	(), {}, []
O	Orders	√  and x²
D	Division	÷, /
M	Multiplication	x, *
A	Addition	+
S	Subtraction	–

1. Brackets: Perform operations inside brackets first.
2. Orders: Evaluate any exponents or powers.
3. Division and Multiplication: Perform division and multiplication from left to right.
4. Addition and Subtraction: Perform addition and subtraction from left to right.

BODMAS Rule Explanation

Let’s consider the expression 12 ÷ 2(1 + 2). Applying the BODMAS rule:

1. Evaluate the expression inside the brackets: 1 + 2 = 3.
2. Perform the division: 12 ÷ 2(3) = 6(3).
3. Perform the multiplication: 6(3) = 18 [Correct Answer]

Solution: 12 ÷ 2(1 + 2) = 12 ÷ 2(3) or 12 ÷ 2 x 3 = 6 x 3 = 18

If we do not follow the given rule, the answer could be different.

12 ÷ 2(1 + 2) = 12 ÷ 2(3)= 12 ÷ 6 = 2 [Wrong Answer]

Note: Don’t be confused by “12 / 2(1 + 2)” in this question.

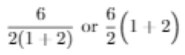
The left expression is 1, and the right one is 9. Those are the two ways to interpret your original question.

To avoid confusion and ensure clear communication, it is highly recommended to use explicit parentheses or clarify the intended order of operations in the original question.

Download PDF Now

BODMAS Rule Questions With Answer

Question 1: Simplify the expression (3+5)-5+2

Solution: (8) – 5 + 2 (First, we perform the addition inside the parentheses:)

3 + 2 = 5 (we perform the subtraction and addition from left to right:)

Question 2: Evaluate the expression: 2 + 3 × (4 – 1) ÷ 5

2 + 3 × (4 – 1) ÷ 5

= 2 + 3 × (3) ÷ 5

= 2 + 3 × 0.6

= 2 + 1.8

= 3.8

Question 3: 8 + (3^2 × 2) – 9 ÷ 9

8 + (3^2 × 2) – 9 ÷ 9

= 8 + (9 × 2) – 9 ÷ 9

= 8 + 18 – 1

= 26 – 1

= 25

Question 4: Evaluate 20 + 6 × 10 ÷ 3 + 4 – 10 ÷ 9 × 2

20 + 6 × 10 ÷ 3 + 4 – 10 ÷ 9 × 2

= 20 + 60 ÷ 3 + 4 – 10 ÷ 9 × 2

= 20 + 20 + 4 – 10 ÷ 9 × 2

= 40 + 4 – 10 ÷ 9 × 2

= 44 – 10 ÷ 9 × 2

= 44 – 1.11 × 2

= 44 – 2.22

= 41.78

Question 5: (3 + 3) x (3 / 3) x (3 × 3)

(3 + 3) × (3 / 3) × (3 × 3)

= 6 × (3 / 3) × (3 × 3)

= 6 × 1 × (3 × 3)

= 6 × 9

= 54

Question 6: 3 × (3 × 3) ÷ 3 ÷ 3 + 3

3 × (3 × 3) ÷ 3 ÷ 3 + 3

= 3 × 9 ÷ 3 ÷ 3 + 3

= 27 ÷ 3 ÷ 3 + 3

= 9 ÷ 3 + 3

= 3 + 3

= 6

Question 7: Evaluate {15 × 32 ÷ 2 × 5} ÷ 75

{15 × 32 ÷ 2 × 5} ÷ 75

= (480 ÷ 2 × 5) ÷ 75

= (240 × 5) ÷ 75

= 1200 ÷ 75

= 16

Question 8: Solve 20 + 30 ÷ 15 × 10 ÷ 10 × (– 3)

20 + 30 ÷ 15 × 10 ÷ 10 × (-3)

= 20 + 2 × (-3)

= 20 + (-6)

= 14

Question 9: 20 – [20 – {10 – (7 – 4 – 3 + 2)}]

20 – [20 – {10 – (7 – 4 – 3 + 2)}]

= 20 – [20 – {10 – 2}]

= 20 – [20 – 8]

= 20 – 12

= 8

Question 10: [(18 – 6) ÷ 4] + [72 – 12 ÷ (3 * 2)]

[(18 – 6) ÷ 4] + [72 – 12 ÷ (3 * 2)]

= [12 ÷ 4] + [72 – 12 ÷ 6]

= 3 + [72 – 2]

= 3 + 70

= 73

Question 11: [50 – 70 ÷ 11 – 2 ]+ ( 10 – 6) ÷ 12

[50 – 70 ÷ 11 – 2] + (10 – 6) ÷ 12

= [50 – 6 – 2] + 4 ÷ 12

= [42] + 4 ÷ 12

= 42 + 0.3333

= 42.3333

Question 12: [{(40 + 50 ÷ 5 × 6) × 2} ÷ ½] × 100

[{(40 + 50 ÷ 5 × 6) × 2} ÷ ½] × 100

= [{(40 + 10 × 6) × 2} ÷ ½] × 100

= [{(40 + 60) × 2} ÷ ½] × 100

= [100 × 2 ÷ ½] × 100

= [200 ÷ ½] × 100

= 400 × 100

= 40,000

Question 13: ⅖ + ¾ × ⅘ ÷ 10/2

⅖ + ¾ × ⅘ ÷ 10/2

= 2/5 + 3/4 × 4/5 ÷ 5

= 2/5 + 3/4 × 4/5 ÷ 5

= 2/5 + 3/4 × 4/5 × 2/10

= 2/5 + 3/4 × 8/50

= 2/5 + 24/200

= 2/5 + 3/25

= (10/25) + (3/25)

= 13/25

= 18 – [6 – {4 – (8 – 9)}] ⇒ 18 – [6 – {4 – (- 1)}]
= 18 – [6 – {4 + 1}] ⇒ 18 – [ 6 – 5]  18 – [ 1] = 18 – 1 = 17

Class 4, 5th BODMAS Questions

• 8 + 3 × 4 – 6 ÷ 2 =
• 5 × (6 + 2) – 4 ÷ 2 =
• (9 – 3) × 2 + 4 ÷ 2 =
• 6 ÷ 3 + 4 × 2 – 5 =
• 12 – (3 + 2) × 2 + 6 ÷ 3 =
• 4 × 2 + 8 ÷ (2 + 1) =
• (7 – 3) × 2 + 6 – 4 ÷ 2 =
• 10 – 2 × (5 + 3) + 4 ÷ 2 =
• 9 ÷ (3 + 2) × (6 – 4) =
• 5 + 2 × 3 – 4 ÷ (8 – 6) =

Class 6, 7th BODMAS Questions

• 12 – 3 × (4 + 2) ÷ 3 =
• 5 × (6 – 2) + 4 ÷ 2 =
• (8 + 2) × 3 – 5 ÷ 5 =
• {(18 ÷ 3) + 4 × 2} – 5 =
• 4 × (6 + 2) ÷ (4 – 2) =
• 8 + 2 × 3 – 4 ÷ (6 – 4) =
• 20 – {3 × (8 – 4)} + 6 ÷ 2 =
• 14 – 2 × (5 + 3) + 6 ÷ 3 =
• 15 – (3 × 2 + 4) ÷ 3 =
• (9 + 2) ÷ {(6 – 4) × 5} =

Class 8, 9th and 10th BODMAS Questions

• 25 – [12 + (6 – 3 × 2) ÷ 4] × 3 =
• (18 – 4) × [5 – (7 – 3 × 2)] ÷ 6 =
• 10 + [4 – (8 + 2 × 3) ÷ 5] × 2 =
• 15 ÷ [6 – (3 + 2) × (4 – 1)] + 7 =
• [9 + (12 – 5) ÷ 2] × [8 – (4 + 1) × 2] =
• (16 – 6) × [5 + (4 – 2) ÷ (8 – 6)] =
• [20 – (5 – 2) × 4] ÷ [6 + (3 – 1) × 2] =
• (9 – 2^2) × (8 – 3 × 2) + 7 =
• 10 + 2 × (4^2 – 5 × 3) ÷ (8 – 2) =
• 3^2 – 4 × (7 – 2^2) + 6 ÷ 3 =
• 2^3 + 4 × 5 – (12 ÷ 6 + 3) =
• Evaluate: [25% of 150] + 20 ÷ 100

Advanced Questions

1. Evaluate the expression: √(25 + 9) – (4 × 3) ÷ 2
2. Evaluate the expression: √(144 + 9) – (9 × 12) ÷ (2 × 3) + √100
3. Simplify the expression: 2^(3 × 2) – 5 × (4 – 1)
4. Evaluate the expression: (7 – 3!) ÷ (2 + 1)
5. Simplify the expression: 4! + 5 × 2^(2 + 1)
6. Evaluate the expression: log(100) + sin(45°) ÷ 2
7. Simplify the expression: (π – 2) × cos(60°) + sqrt(16)
8. Evaluate the expression: (e^(2 + 3) – ln(10)) ÷ (sin(30°) + cos(45°))
9. Simplify the expression: log(1000) – log(10) + tan(60°) × 3
10. Evaluate the expression: (2^(3 × 2) + √(16)) ÷ (log(100) – sin(45°))
11. Simplify the expression: (cos(30°) + tan(45°)) × (3 – log(100))

From this, it can be concluded that learning and applying the BODMAS rule is the correct way to maintain consistency in mathematical operations and avoid errors. It provides a standardized approach to evaluating mathematical expressions, which allows us to solve our mathematical problems more effectively.

• Maths Book PDF – UPSC Optional, IIT JEE, B.SC, B.A, Engineering